Daftar Isi
Pengertian
Dalam ilmu matematika terdapat materi pembelajaran mengenai perbandingan. Materi perbandingan juga termasuk kedalam golongan aritmatika.
Maka dari itu perbandingan dapat diartikan sebagai usaha membandingkan dua objek atau lebih dengan menggunakan rumus perbandingan yang tepat.
Perbandingan dapat dibagi menjadi 2 yakni perbandingan senilai dan perbandingan berbalik nilai.
Dalam rumus perbandingan senilai ataupun berbalik nilai dapat diselesaikan dengan cara aritmatika.
Apabila kita lebih mendalami dan memahami materi ini, maka akan sangat berguna dalam kehidupan kita sehari hari. Contohnyanya membandingkan jarak kota A dan kota B, membandingkan tinggi badan anak A dengan B, dan sebagainya.
Rumus Perbandingan Senilai
Perbandingan senilai merupakan upaya membandingkan dua objek atau lebih dimana jika besar salah satu nilai variabel bertambah, maka nilai variabel lain menjadi bertambah juga.
Maka perbandingan senilai memmiliki jumlah nilai variabel yang sama. Untuk lebih jelasnya dapat kita simak rumus perbandingan senilai dibawah ini:

Dari persamaan di atas dapat kita peroleh
| Persamaan | Keterangan |
 | Semakin besar nilai b1, maka semakin besar pula nilai a1 |
 | Semakin besar nilai a1, maka semakin besar pula nilai b1 |
 | Semakin besar nilai b2, maka semakin besar pula nilai a2 |
 | Semakin besar nilai a2, maka semakin besar pula nilai b2 |
Berdasarkan rumus perbandingan diatas dapat disimpulkan bahwa nilai a1 sebanding dengan b1 dan nilai a2 sebanding dengan b2.
Perbandingan Berbalik Nilai
Perbandingan berbalik merupakan upaya membandingkan dua objek atau lebih dimana jika besar nilai salah satu variabel bertambah, maka nilai variabel lain menjadi berkurang.
Untuk lebih jelasnya dapat kita simak rumus perbandingan berbalik nilai dibawah ini:

Dari persamaan di atas dapat kita peroleh
| Persamaan | Keterangan |
 | Semakin besar nilai b1, maka semakin kecil nilai a1 |
 | Semakin besar nilai a1, maka semakin kecil nilai b1 |
 | Semakin besar nilai b2, maka semakin kecil nilai a2 |
 | Semakin besar nilai a2, maka semakin kecil nilai b2 |
Berdasarkan rumus perbandingan diatas dapat disimpulkan bahwa nilai a1 berbanding terbalik dengan nilai b2 dan nilai a2 berbanding terbalik dengan nilai b1.
Contoh Soal Perbandingan
Berikut adalah contoh soal Perbandingan dan pembahasannya:
Dalam sebuah divisi kantor ada 7 orang pekerja dengan gaji seluruh pekerja sebesar Rp 21.000.000. Karena kekurangan orang, divisi tersebut menambahkan 3 orang lagi. Berapa jumlah gaji yang harus dikeluarkan seluruh pekerja divisi tersebut setelah penambahan karyawan ?
Jawab
Diketahui:
a1 = 7
b1 = 21.000.000
a2 = 7 + 3 = 10
Ditanya ; b2 = ?
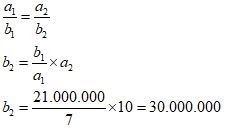
Jadi jumlah gaji seluruh karyawan divisi tersebut setelah penambahan karyawan adalah sebesar Rp 30.000.000.
20 menu nasi goreng A dimasak oleh 8 koki dalam 30 menit. Jika koki menambahkan 4 koki lagi, berapa waktu yang dibutuhkan untuk memasak 20 menu nasi goreng A? dan berapa menu nasi goreng A yang bisa diselesaikan dalam waktu 30 menit setelah penambahan koki?
Jawab ;
Diketahui ;
a1 = 20
b1 = 8
c1 = 30
b2 = 8 + 4 = 12
Ditanya ;
c2 & a2 = ?

Jadi waktu yang dibutuhkan untuk memasak 20 menu nasi goreng A setelah koki ditambah adalah 20 menit.

Jadi menu nasi goreng A yang dapat dibuat dalam 30 menit setelah penambahan koki adalah sebanyak 30 piring.
Demikian sedikit pembahasan tentang rumus perbandingan. Biar lebih mahir, yuk latihan di soal perbandingan ya. Selamat belajar