Perbandingan Trigonometri – Trigonometri adalah cabang ilmu matematika yang mempelajari tentang sudut, sisi, dan perbandingan antara sudut pada sisi.
Dasarnya memakai bangun datar segitiga.
Untuk lebih memahami perbandingan trigonometri, Simak pembahasan dibawah ini.

- Sisi AC merupakan sisi miring segitiga
- Sisi BC merupakan sisi depan sudut
- Sisi AB merupakan sisi samping sudut α
Di sini kita akan mengenal istilah matematika baru, yaitu sinus (sin), cosinus (cos), tangent (tan), cosecan (csc), secan (sec) dan cotangent (cot).
- Sinus merupakan kebalikan dari cosecan
- cosinus kebalikan dari secan
- tangent kebalikan dari cotangent
Sinus, Cosinus dan Tangent digunakan untuk menghitung sudut dengan perbandingan trigonometri sisi di segitiga.
Dengan gambar segitiga diatas, nilai Sinus, Cosinus dan Tangent diperoleh dengan cara sebagai berikut:

Daftar Isi
Sudut Istimewa
Berikut ini nilai sin, cos, dan tan untuk sudut istimewa:
| 0o | 30o | 45o | 60o | 90o | |
| Sin | 0 | ½ | ½√2 | ½√3 | 1 |
| Cos | 1 | ½√3 | ½√2 | ½ | 0 |
| Tan | 0 | ⅓√3 | 1 | √3 | – |
Dalam Kuadran
Sudut dalam suatu lingkaran, memiliki rentang 0° – 360°, sudut tersebut dibagi menjadi 4 kuadran, dengan masing-masing kuadran memiliki rentang sebesar 90°.

Kuadran I
Memiliki rentang sudut dari 0° – 90° dengan nilai sinus, cosinus dan tangent positif.
Kuadran II
Memiliki rentang sudut dari 90° – 180° dengan nilai cosinus dan tangen negatif, sinus positif.
Kuadran III
Memiliki rentang sudut dari 180° – 270° dengan nilai sinus dan cosinus negatif, tangen positif.
Kuadran IV
Memiliki rentang sudut dari 270° – 360° dengan nilai sinus dan tangent negatif, cosinus positif.
Perhatikan tabel trigonometri di bawah ini:
Tabel Trigonometri
| Kuadran I | Kuadran II | Kuadran III | Kuadran IV | |
| Sin α | Cos (90 – α) | Sin (180 – α) | –Sin (180 + α) | –Sin (360 – α) |
| Cos α | Sin (90 – α) | –Cos (180 – α) | –Cos (180 + α) | Cos (360 – α) |
| Tan α | Cotan (90 – α) | –Tan (180 – α) | Tan (180 + α) | –Tan (360 – α) |
| Cosec α | Sec (90 – α) | Cosec (180 – α) | –Cosec (180 + α) | –Cosec (360 – α) |
| Sec α | Cosec (90 – α) | –Sec (180 – α) | –Sec (180 + α) | Sec (360 – α) |
| Cotan α | Cotan (90 – α) | –Cotan (180 – α) | Cotan (180 + α) | –Cotan (360 – α) |
Identitas Trigonometri
Dalam segitiga siku-siku, selalu berlaku prinsip phytagoras, yaitu a2+b2 = c2.
Prinsip phytagoras tersebut menjadi asal pembuktian identitas trigonometri.
a2+b2 = c2
bagi kedua ruas dengan c2, diperoleh persamaan baru

Sederhanakan dengan sifat eksponensial menjadi

Subtitusi bagian yang sesuai dengan perbandingan trigonometri pada segitiga, sehingga diperoleh
(sin α)2 + (cos α)2 = 1
atau bisa ditulis menjadi
sin2 α + cos2 α = 1
Dari identitas yang pertama, dapat diperoleh bentuk lainnya, yaitu:
1. Bagi kedua ruas dengan cos2 α, diperoleh
(sin2 α)/(cos2 α) + 1 = 1/(cos2 α)
Karena
(sin2 α)/(cos2 α) = tan2 α dan 1/(cos2 α) = sec2 α
maka diperoleh
tan2 α + 1 = sec2 α
2. Bagi kedua ruas dengan sin2 α, diperoleh
1 + (cos2 α)/(sin2 α) = 1/(sin2 α)
Karena
(cos2 α)/(sin2 α) = cot2 α dan 1/(sin2 α) = csc2 α
maka diperoleh
1 + cot2 α = csc2 α
Perbandingan Trigonometri Untuk Sudut Khusus
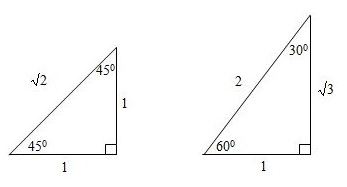
Berdasarkan gambar diatas bisa ditentukan nilai perbandingan trigonometri sudut-sudut khusus itu dalam tabel sebagai berikut.

*td: tak terdefinisi
Contoh Soal Trigonometri
Tentukanlah nilai dari sin 120°+cos 201°+cos 315°!
Jawab:
sin 120° ada di kuadran II, hingga nilainya tetap positif dengan besar sama seperti sin 60°
sin 120° = sin (180-60)° = sin 60° = 1/2 √3
cos 120° ada di kuadran III, hingga nilainya negatif dengan besar sama seperti cos 30°
cos 120° = cos (180+30)° = – cos 30° = -1/2 √3
cos 315° ada di kuadran IV, hingga nilainya positif dengan besar sama seperti cos 45°
cos 315° = cos (360-45)° = cos 45° = 1/2 √2
Diketahui segitiga siku-siku ABC, siku-siku di C, panjang a = 4 dan b = 3.
Tentukanlah panjang sisi dan nilai perbandingan trigonometri sudut α
Jawab:
