Kali ini kita akan membahas tentang statistik deskriptif mulai dari pengertian, jenis – jenis, dan contoh soal statistik dekriptif beserta pembahasannya.
Daftar Isi
Pengertian Statistik
Statistika / Statistik adalah suatu ilmu yang mempelajari tentang cara – cara pengumpulan data, penyajian data, analisis dan interpretasi tentang data tersebut.
Seorang yang belajar statistika biasanya bekerja dengan data numerik yang berupa hasil cacahan ataupun hasil pengukuran, atau dengan data yang diklasifikasikan menurut kriteria tertentu.
Setiap informasi yang tercatat dan terkumpul, baik numerik dan kategorik disebut juga dengan pengamatan.
Metode statistika yaitu prosedur – prosedur yang digunakan dalam pegumpulan, penyajian, analisis, dan penafsiran data.
Pengertian Statistik Deskriptif
Statistik deskriptif adalah metode – metode yang berkaitan dengan pengumpulan dan Penyajian suatu gugus data sehingga dapat memberikan informasi yang berguna.
Statistik Deskriptif merupakan metode yang sederhana. Metode ini hanya mendeskripsikan kondisi dari data yang sudah dimiliki Dan menyajikannya dalam bentuk tabel diagram grafik dalam uraian – uraian singkat dan juga terbatas.
Materi Statistik Deskriptif
Penyajian data kategori deskriptif dapat berbentuk grafis dan numerik, yaitu antara lain :
1. Penyajian Data Dalam Bentuk Grafis
Penyajian data dalam bentuk grafis terdiri dari beberapa macam, yaitu :
Histogram
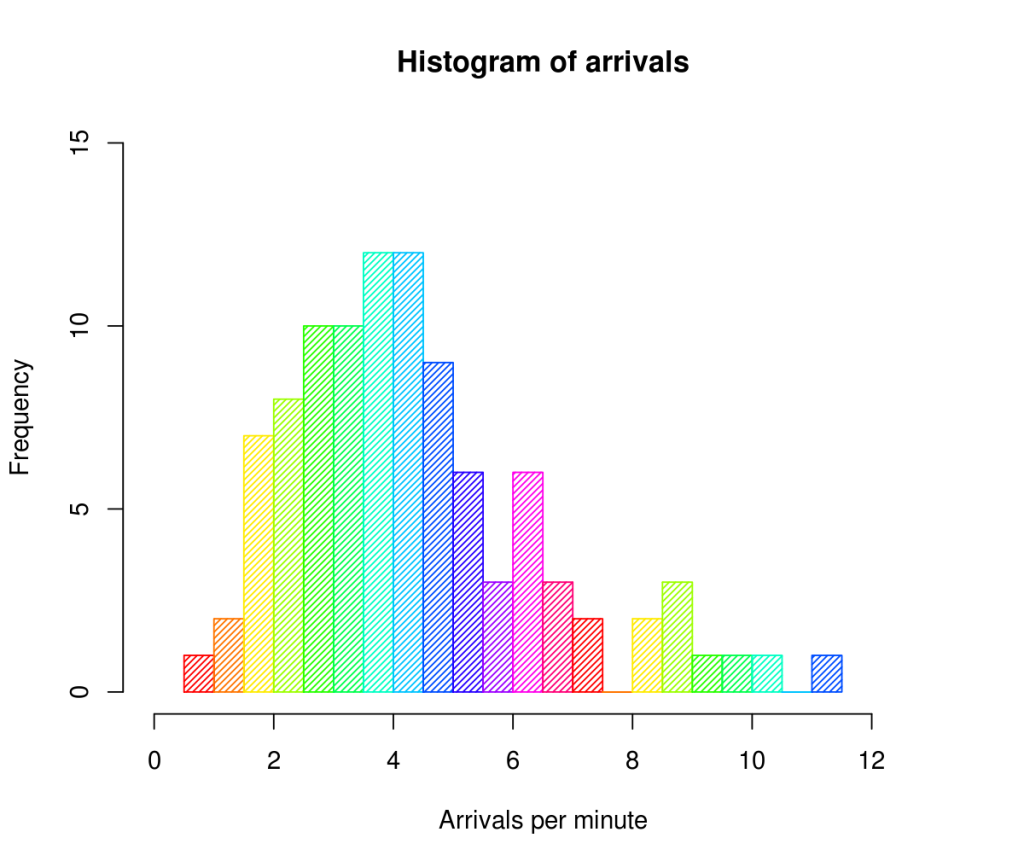
Histogram merupakan grafik dari distribusi frekuensi suatu variabel. Tampilan histogram berupa balok.
Penyajian data ini terdiri dari dua sumbu utama dengan sudut 90o, sumbu X sebagai absis dan sumbu Y sebagai ordinat.
Lebar balok yaitu merupakan jarak dari batas kelas interval, sedangkan tinggi balok menunjukkan besarnya frekuensi.
Pie Chart

Pie Chart (Diagram kue) adalah diagram lingkaran yang dibagi menjadi beberapa sektor.
Tiap sektor dapat menyatakan besarnya presentase atau bagian untuk masing-masing kelompok.
Poligon

Poligon adalah grafik dari distribusi frekuensi tergolong suatu variabel.
Tampilan poligon juga berupa garis – garis patah yang diperoleh dengan cara menghubungkan puncak masing – masing nilai tengah kelas.
Poligon sangat baik digunakan untuk membandingkan bentuk dari dua distribusi.
Ogive

Ogive merupakan grafik yang menggambarkan distribusi frekuensi kumulatif suatu variabel.
Untuk suatu tabel distribusi frekuensi, dapat juga dibuat ogive positif dan ogive negatifnya.
Diagram Batang Daun (Stem and Leaf)
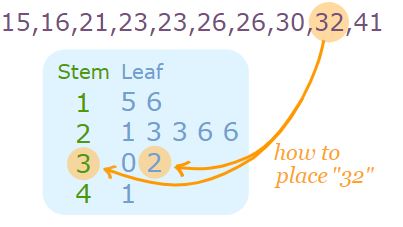
Diagram Batang Daun (Stem and Leaf) hampir sama dengan histogram, hanya saja informasi yang diperoleh lebih baik karena diagram batang daun memperlihatkan nilai – nilai hasil pengamatan asli.
Dalam diagram ini ditampilkan bilangan – bilangan yang juga sebagai batang dan disebelah kananya ditulis bilangan sisanya.
2. Penyajian Data Numerik
Penyajian data secara numerik terdiri dari beberapa macam, yaitu:
Ukuran Pemusatan Data (Central Tredency)

Salah satu aspek yang paling penting untuk menggambarkan distribusi data adalah nilai pusat data pengamatan (tendensi sentral).
Setiap pengukuran aritmatika yang ditujukan untuk menggambarkan suatu nilai yang mewakili nilai pusat atau nilai sentral dari suatu gugus data (himpunan pengamatan) dikenal sebagai ukuran tendensi sentral.
Terdapat tiga ukuran tendensi sentral yang sering digunakan, yaitu:
- Mean (Rata-rata hitung/rata-rata aritmetika)
- Median
- Mode
Dispersion (Dispersi)

Dalam statistik, dispersi adalah sejauh mana suatu distribusi ditarik atau dipencar.
Contoh umum ukuran dispersi statistik adalah varians, standar deviasi, dan rentang interkuartil.
Fractile (Fractal)

Fractal adalah pola grafik dari analisis teknikal, biasanya digunakan oleh trader dalam menentukan entry dan exit point ke/dari pasar.
Agar mendapatkan titik yang lebih akurat, fractal sering digunakan untuk menghubungkan indikator-indikator yang berbeda dan metode analisis teknikal lainnya, karena dianggap sebagai lagging indikator yang mengikuti tren.
Fractal terdiri atas lima lilin, dengan nilai rata-ratanya menunjukkan harga maksimum atau minimum pada jangka waktu tertentu.
Skewness

Skewness (ukuran kemiringan) merupakan suatu bilangan yang dapat menunjukan miring atau tidaknya bentuk kurva suatu distribusi frekuensi.
Skewness adalah derajat ketidaksimetrisan suatu distribusi.
Jika kurva frekuensi suatu distribusi memiliki ekor yang lebih memanjang ke kanan (dilihat dari meannya) maka dikatakan menceng kanan (positif) dan jika sebaliknya maka menceng kiri (negatif).
Secara perhitungan, skewness adalah momen ketiga terhadap mean.
Distribusi normal (dan distribusi simetris lainnya, misalnya distribusi t atau Cauchy) memiliki skewness 0 (nol).
| Batas – Batas nilai ukuran kemiringan | Keterangan |
| 0 ≤ | Sk = α3 | < 0,1 | bentuk kurva DF dianggap normal |
| 0,1 ≤ | Sk = α3 | < 0,3 | bentuk kurva DF miring ke kiri atau kanan |
| 0,3 ≤ | Sk = α3 | | bentuk kurva DF sangat miring ke kiri atau kanan |
Pengukuran Keruncingan (Kurtosis)

Pengukuran kurtosis (peruncingan) sebuah distribusi teoritis adakalanya dinamakam pengukuran ekses (excess) dari sebuah distribusi.
Sebenarnya kurtosis bisa dianggap sebagai suatu distorsi dari kurva normal.
Keruncingan atau kurtosis adalah tingkat ketinggian puncak atau keruncingan dari sebuah distribusi yang biasanya diambil secara relatif terhadap suatu distribusi normal.
Berdasarkan keruncingannya, kurva distribusi dapat dibedakan atas tiga macam, yaitu sebagai berikut:
- Leptokurtik: merupakan distribusi yang memiliki puncak relatif tinggi
- Platikurtik: merupakan distribusi yang memiliki puncak hampir mendatar
- Mesokurtik: merupakan distribusi yang memiliki puncak tidak tinggi dan tidak mendatar. Bila distribusi merupakan distribusi simetris, maka distribusi mesokurtik dianggap sebagai distribusi normal.
Demikian pembahasan tentang Statistik Deskriptif, semoga bermanfaat.